Wenn man über statistisch belegbare Zusammenhänge stolpert, stolpert man auch oft darüber, dass eine Korrelation noch keine Kausalität bedeutet. Wenn man eine absolut zufällige Menge von Menschen auswählt, kann man zum Beispiel unwiderlegbar zeigen, dass mit höherem Testosteronspiegel statistisch gesehen größere Füße einhergehen.
Der geübte Leser wird das Problem schnell erkennen: Männer haben im Schnitt einen höheren Testosteronspiegel und größere Füße als Frauen. (Das bei einer zufälligen Auswahl auch Kinder vorkommen werden, sollte man übrigens auch nicht vergessen).
Sehr amüsant auch die Erkenntnis, dass die Lernleistung eines Schülers von der Länge des Bücherregals in seinem Kinderzimmer abhängt.
Im Englischen Raum ist das Ganze sogar ein geflügeltes Wort „Correlation does not imply causation“, das in Diskussionen zu diversen Ergüssen in den Medien gerne mal in den Raum geworfen wird. Das „deutsche“ Pendant „cum hoc ergo propter hoc“ ist im Vergleich wohl eher unbekannt. Vermutlich, weil der lateinische Text nicht so zugänglich ist.
Die Phrase trifft sicher oft genug zu: wenn man eine merkwürdige Folgerung aufgrund von Korrelation sieht, kann man sich fragen, ob dieser Grundsatz nicht zutrifft. Man muss aber auch umgekehrt vorsichtig sein. Auch wenn aus Korrelation nicht direkt Kausalität gefolgert werden kann, kann sie doch einen Hinweis geben, dass da irgendwo ein Zusammenhang vorhanden ist. Was sich nicht prinzipiell ausschließt, könnte ebenso eine kausale Beziehung haben.
Nicht unbedingt der, den man direkt gefunden hat, sondern ein anderer; die gefundene Korrelation gibt dann nur einen Hinweis auf die Existenz/Art der zugrunde liegenden Kausalität. Im obigen Fall erscheint es logisch anzunehmen, dass ein längeres Bücherregal einfach bedeutet, dass das Kind mehr Bücher hat, mehr liest und vielleicht auch einfach mehr lernt. Stößt man also auf eine solche Korrelation, die zwar unsinnig scheint, kann man trotzdem weitere Untersuchungen anstellen, um den Grund zu finden. Im Beispiel mit dem Testosteron und den Füßen muss man dahinterkommen, dass man zwei Gruppen (unter Berücksichtigung des Alters natürlich), Männer und Frauen, hat, die man getrennt betrachten muss.
Der Autor Daniel Engber hat sich nun (unter anderem) mit der Frage beschäftigt, wer als Erster die Englische Phrase geprägt hat.
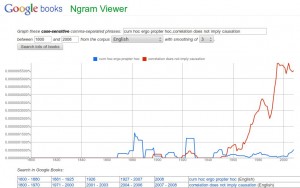Er suchte dabei in von Google digitalisierten Büchern nach dem Auftauchen von Varianten von „correlation does not imply causality“ (rot), die offenbar um 1890 auftauchten. Das lateinische „cum hoc ergo propter hoc“ (blau) betrachtete er jedoch nicht; eine google Books Suche findet es bereits in einem Werk von 1739. Dieses vereinzelte Ergebnis sieht man im Diagramm auf der Seite nicht.
Er folgert aus der zeitlichen Korrelation, dass das Auftauchen der Phrase und die danach steigende Häufigkeit der Nutzung wohl mit dem Korrelationskoeffizienten, der vom ideologisch ziemlich braunen britischen Mathematiker Karl Pearson ausformuliert wurde, zusammenhängt. Pearson war der erste, der das Prinzip in mathematisch klare Form goss.
Der Korrelationskoeffizient ist dabei dem Betrage nach eine Zahl zwischen 0 und 1, die quasi die Stärke der Korrelation beschreibt. Je näher der Wert bei 0 liegt, desto kleiner der lineare Zusammenhang. Bei 1 hätte man einen sicheren Zusammenhang.
Mit der Einführung der mathematischen Grundlage für Korrelation als „Beweismittel“, von der Pearson selbst wusste, dass sie problematisch sein konnte:
All causation as we have defined it is correlation, but the converse is not necessarily true, i.e. where we find correlation we cannot always predict causation. In a mixed African population of Kaffirs and Europeans, the former may be more subject to smallpox, yet it would be useless to assert darkness of skin (and not absence of vaccination) as a cause.
,
wurde es auch wichtiger, auf das Problem dabei hinzuweisen.
Seitdem ist die Nutzung der Phrase, zumindest der Englischen, immer stärker gestiegen. Offenbar kennen immer mehr Menschen diesen Argumentationsfehler und weisen daraufhin.
Lustig wird es, wenn das als Argument gegen die Ergebnisse von Interventionsstudien hervorgewürgt wird.
Immer wieder schön auch:
http://ecx.images-amazon.com/images/I/41YCzjnQTRL._BO2,204,203,200_PIsitb-sticker-arrow-click,TopRight,35,-76_AA300_SH20_OU03_.jpg
Sich dieses Argumentationsfehlers bewusst zu sein kann in seiner Bedeutung kaum überschätzt zu werden. Ich habe selbst in Wissenschaftsteilen von Zeitungen oder Zeitschriften oft den Eindruck, dass dieser Fehler gemacht wird. Zum Beispiel wenn es um die vermeindlich negative Wirkung von Fernseh- oder Computerspielekonsum durch Kinder geht. Die Erkenntnis, dass ein hoher Fernsehkonsum mit schlechten Schulleistungen korreliert, heißt eben nicht, dass für die schlechten Schulleistungen der Fernsehkonsum ursächlich ist. Viel wahrscheinlicher scheint mir, dass „klügere“ Eltern ihre Kinder i.d.R. weniger vor den Fernseher setzen. Die Kausalkette wäre dann: „Kluge“ Eltern —> gute Schulleitstungen der Kinder…
Und die Pastafarians haben auch festgestellt, dass die Zahl der Piraten auf den Weltmeeren invers mit der Erderwärmung korreliert
http://www.google.at/imgres?imgurl=http://www.venganza.org/images/PiratesVsTemp.png&imgrefurl=http://www.venganza.org/about/open-letter/&h=400&w=600&sz=44&tbnid=CJY-fTYNFdoUPM:&tbnh=82&tbnw=123&zoom=1&usg=__wxh3qJNFKcx8-ZBG7Mp-V9_L3lg=&docid=61leGrj9nauRFM&hl=de&sa=X&ei=iYltUIqqBM_KswbkiIDQDQ&ved=0CD8Q9QEwAw&dur=10621
Bekanntlich haben Männer mit weniger Haaren höhere Gehälter.
In unseren Breiten uns sind die wärmeren Tage auch die längeren Tage -> wegen der Wärmeausdehnung.
Nach Dilbert stimmt das mit den Haaren nicht.
ich hoffe doch dass die glatzköpfigen Neonazis max Hartz4 haben und nicht in Aufsichtsräten sitzen
Ich hab da mal ne dumme Frage: Was hat die ideologische Ausrichtung des Mathematikers Pearson mit dem behandelten Thema zu tun?
Gibt es etwa eine Korrelation zwischen „ziemlich brauner“ Ideologie und Statistik/Mathematik/britischen Wissenschaftlern? Oder gibt es einen kausalen Zusammenhang? Oder warum glaubte der Autor des Beitrags, das erwähnen zu müssen?
@Ernst
Ich denke nicht, dass die ideologische Ausrichtung von Pearson erwähnt worden ist, um seine Sachaussagen zu diskreditieren, sondern eher um anzudeuten, dass die Ideologie nicht gegen seine Sachaussage ins Feld geführt werden kann. Aus der Erkenntnistheorie eines Autors lässt sich allgemein nicht unmittelbar auf die jeweilige politische Haltung ihres Verfechters schließen; das ist ein weiter Weg.
Der Korrelationskoeffizient geht übrigens von – 1 bis +1, wobei – 1 besser als 0.8 ist.
Mist. Eigentlich war das als Vereinfachung gedacht, dass es überhaupt verständlich ist.
Wieso, stimmt doch:
Der Korrelationskoeffizient ist dabei dem [b]Betrage[b] nach eine Zahl zwischen 0 und 1 …
Btw.: „-1 besser als -0.8“: Besser ist im Verständnisssinne ein leicht komisches Wort 😉
Die Korrelation ist bei -1 stärker als bei -0,8 und bei 0 am Schwächsten. Nur ist die Korrelation bei negativen Werten umgekehrt. Mir fällt gerade kein gutes Beispiel ein, vielleicht:
Trockene Straße korreliert stark mit Regen, aber der Koeffizient ist negativ. Wenn die Straße trocken ist, wird es wahrscheinlich NICHT geregnet haben.